Círculo de Fuhrmann
Em geometria, o círculo de Fuhrmann de um triângulo, denominado em memória do matemático alemão Wilhelm Fuhrmann (1833–1904), é o círculo com um diâmetro do segmento de reta entre o ortocentro e o ponto de Nagel . Este círculo é idêntico ao circuncírculo do triângulo de Fuhrmann.[1]
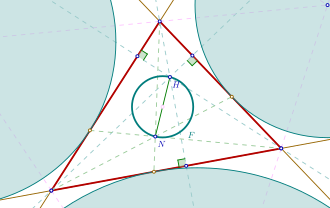

ponto de Nagel e ortocentro
O raio de círculo de Fuhrmann de um triângulo com lados a, b e c e circunraio R (raio da circunferência circunscrita) é
que é também a distância entre o circuncentro e o incentro.[2]
Além do ortocentro, o círculo de Fuhrmann cruza cada altitude do triângulo em um ponto adicional. Todos esses pontos têm distância de seus vértices associados do triângulo. Aqui denota o raio dos triângulos inscritos.[3]
Referências
- ↑ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, pp. 228–229, 300 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- ↑ Weisstein, Eric W. «Fuhrmann Circle». MathWorld (em inglês)
- ↑ Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 49-52
Leitura adicional
editar- Nguyen Thanh Dung: "The Feuerbach Point and the Fuhrmann Triangle". Forum Geometricorum, Volume 16 (2016), pp. 299–311.
- J. A. Scott: An Eight-Point Circle. In: The Mathematical Gazette, Volume 86, No. 506 (Jul., 2002), pp. 326–328 (JSTOR)





