Demônio de Maxwell
O demônio de Maxwell é um experimento mental que parece refutar a segunda lei da termodinâmica. Foi proposto pelo físico James Clerk Maxwell em 1867.[1] Em sua primeira carta, Maxwell se referiu à entidade como um "ser finito" ou um "ser que pode jogar um jogo de habilidade com as moléculas". Lord Kelvin mais tarde o chamaria de "demônio".[2]
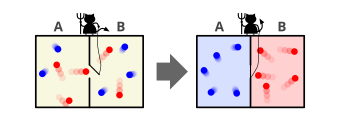
No experimento mental, um demônio controla uma porta entre duas câmaras contendo um gás. Conforme moléculas individuais de gás (ou átomos) se aproximam da porta, o demônio rapidamente abre e fecha a porta para permitir que apenas moléculas de movimento rápido passem em uma direção, e apenas moléculas de movimento lento passem na outra. Como a temperatura cinética de um gás depende das velocidades de suas moléculas constituintes, as ações do demônio fazem com que uma câmara aqueça e a outra esfrie. Isso diminuiria a entropia total do sistema, aparentemente sem aplicar nenhum trabalho, violando assim a segunda lei da termodinâmica.
O conceito do demônio de Maxwell provocou um debate substancial na filosofia da ciência e na física teórica, que continua até os dias atuais. Ele estimulou o trabalho sobre a relação entre a termodinâmica e a teoria da informação. A maioria dos cientistas argumenta que, em bases teóricas, nenhum dispositivo prático pode violar a segunda lei dessa forma. Outros pesquisadores implementaram formas do demônio de Maxwell em experimentos, embora todos eles difiram do experimento mental até certo ponto e nenhum tenha demonstrado violar a segunda lei.
Origem e história da ideia
editarO experimento mental apareceu pela primeira vez em uma carta que Maxwell escreveu a Peter Guthrie Tait em 11 de dezembro de 1867. Ele apareceu novamente em uma carta a John William Strutt em 1871, antes de ser apresentado ao público no livro de Maxwell de 1872 sobre termodinâmica intitulado Teoria do Calor.[3]
Em suas cartas e livros, Maxwell descreveu o agente abrindo a porta entre as câmaras como um "ser finito". Sendo um homem profundamente religioso, ele nunca usou a palavra "demônio". Em vez disso, William Thomson (Lord Kelvin) foi o primeiro a usá-la para o conceito de Maxwell, no periódico Nature em 1874, e deu a entender que pretendia a interpretação da mitologia grega de um daemon, um ser sobrenatural trabalhando em segundo plano, em vez de um ser malévolo.[2][4][5]
Experimento mental original
editarA segunda lei da termodinâmica assegura (através da probabilidade estatística) que dois corpos de temperaturas diferentes, quando colocados em contato um com o outro e isolados do resto do Universo, evoluirão para um equilíbrio termodinâmico no qual ambos os corpos têm aproximadamente a mesma temperatura.[6] A segunda lei também é expressa como a afirmação de que em um sistema isolado, a entropia nunca diminui.[6]
Maxwell concebeu um experimento mental como uma forma de promover a compreensão da segunda lei. Sua descrição do experimento é a seguinte:[6][7]
... se concebermos um ser cujas faculdades são tão aguçadas que ele pode seguir cada molécula em seu curso, tal ser, cujos atributos são tão essencialmente finitos quanto os nossos, seria capaz de fazer o que é impossível para nós. Pois vimos que moléculas em um recipiente cheio de ar a uma temperatura uniforme estão se movendo com velocidades de modo algum uniformes, embora a velocidade média de qualquer grande número delas, arbitrariamente selecionada, seja quase exatamente uniforme. Agora, vamos supor que tal recipiente seja dividido em duas porções, A e B, por uma divisão na qual há um pequeno orifício, e que um ser, que pode ver as moléculas individuais, abre e fecha esse orifício, de modo a permitir que apenas as moléculas mais rápidas passem de A para B, e apenas as moléculas mais lentas passem de B para A. Ele irá, assim, sem dispêndio de trabalho, aumentar a temperatura de B e diminuir a de A, em contradição com a segunda lei da termodinâmica.
Em outras palavras, Maxwell imagina um recipiente dividido em duas partes, A e B.[6][8] Ambas as partes são preenchidas com o mesmo gás em temperaturas iguais e colocadas uma ao lado da outra. Observando as moléculas em ambos os lados, um demônio imaginário guarda um alçapão entre as duas partes. Quando uma molécula mais rápida que a média de A voa em direção ao alçapão, o demônio a abre, e a molécula voará de A para B. Da mesma forma, quando uma molécula mais lenta que a média de B voa em direção ao alçapão, o demônio a deixará passar de B para A. A velocidade média das moléculas em B terá aumentado enquanto em A elas terão desacelerado em média. Como a velocidade molecular média corresponde à temperatura, a temperatura diminui em A e aumenta em B, contrariando a segunda lei da termodinâmica. Uma máquina térmica operando entre os reservatórios térmicos A e B poderia extrair trabalho útil dessa diferença de temperatura.
O demônio deve permitir que as moléculas passem em ambas as direções para produzir apenas uma diferença de temperatura; a passagem unidirecional de moléculas mais rápidas que a média de A para B causará o desenvolvimento de temperaturas e pressões mais altas no lado B.
Críticas e desenvolvimento
editarVários físicos apresentaram cálculos que mostram que a segunda lei da termodinâmica não será realmente violada, se uma análise mais completa for feita de todo o sistema, incluindo o demônio.[6][8][9] A essência do argumento físico é mostrar, por cálculo, que qualquer demônio deve "gerar" mais entropia segregando as moléculas do que poderia eliminar pelo método descrito. Ou seja, seria necessário mais trabalho termodinâmico para avaliar a velocidade das moléculas e seletivamente permitir que elas passassem pela abertura entre A e B do que a quantidade de energia ganha pela diferença de temperatura causada por isso.
Uma das respostas mais famosas a essa questão foi sugerida em 1929 por Leó Szilárd,[10] e mais tarde por Léon Brillouin.[6][8] Szilárd apontou que um demônio de Maxwell da vida real precisaria ter algum meio de medir a velocidade molecular e que o ato de adquirir informações exigiria um gasto de energia. Como o demônio e o gás estão interagindo, devemos considerar a entropia total do gás e do demônio combinados. O gasto de energia pelo demônio causará um aumento na entropia do demônio, que será maior do que a redução da entropia do gás.
Em 1960, Rolf Landauer levantou uma exceção a esse argumento.[6][8][11] Ele percebeu que alguns processos de medição não precisam aumentar a entropia termodinâmica, desde que sejam termodinamicamente reversíveis. Ele sugeriu que essas medições "reversíveis" poderiam ser usadas para classificar as moléculas, violando a Segunda Lei. No entanto, devido à conexão entre entropia na termodinâmica e teoria da informação, isso também significava que a medição registrada não deve ser apagada. Em outras palavras, para determinar se deve deixar uma molécula passar, o demônio deve adquirir informações sobre o estado da molécula e descartá-la ou armazená-la. Descartá-la leva ao aumento imediato da entropia, mas o demônio não pode armazená-la indefinidamente. Em 1982, Charles Bennett mostrou que, por mais bem preparado que seja, eventualmente o demônio ficará sem espaço de armazenamento de informações e deve começar a apagar as informações que coletou anteriormente.[8][12] Apagar informações é um processo termodinamicamente irreversível que aumenta a entropia de um sistema. Embora Bennett tenha chegado à mesma conclusão do artigo de Szilard de 1929, de que um demônio maxwelliano não poderia violar a segunda lei porque a entropia seria criada, ele chegou a ela por razões diferentes. Em relação ao princípio de Landauer, a energia mínima dissipada pela exclusão de informações foi medida experimentalmente por Eric Lutz et al. em 2012. Além disso, Lutz et al. confirmaram que, para se aproximar do limite de Landauer, o sistema deve se aproximar assintoticamente da velocidade de processamento zero.[13] Recentemente, o princípio de Landauer também foi invocado para resolver um paradoxo da física estatística aparentemente não relacionado, o paradoxo de Loschmidt. [14]
John Earman e John D. Norton argumentaram que as explicações de Szilárd e Landauer sobre o demônio de Maxwell começam assumindo que a segunda lei da termodinâmica não pode ser violada pelo demônio, e derivam outras propriedades do demônio dessa suposição, incluindo a necessidade de consumir energia ao apagar informações, etc.[15][16] Portanto, seria circular invocar essas propriedades derivadas para defender a segunda lei do argumento demoníaco. Bennett mais tarde reconheceu a validade do argumento de Earman e Norton, ao mesmo tempo em que sustentava que o princípio de Landauer explica o mecanismo pelo qual sistemas reais não violam a segunda lei da termodinâmica.[17]
Progresso recente
editarEmbora o argumento de Landauer e Bennett responda apenas à consistência entre a segunda lei da termodinâmica e todo o processo cíclico de todo o sistema de uma máquina de Szilard (um sistema composto da máquina e do demônio), uma abordagem recente baseada na termodinâmica que não é de equilíbrio para pequenos sistemas flutuantes forneceu uma visão mais profunda de cada processo de informação com cada subsistema. Deste ponto de vista, o processo de medição é considerado um processo onde a correlação (informação mútua) entre a máquina e o demônio aumenta, diminuindo a entropia do sistema em uma quantidade dada pela informação mútua.[18] Se a correlação muda, relações termodinâmicas como a segunda lei da termodinâmica e o teorema da flutuação para cada subsistema devem ser modificadas, e para o caso de controle externo uma segunda lei como desigualdade[18][19][20] e um teorema de flutuação generalizado[21] com informação mútua são satisfeitos. Para processos de informação mais gerais, incluindo processamento de informação biológica, tanto a desigualdade[22] quanto a igualdade[23] com informação mútua são válidas. Quando medições repetidas são realizadas, a redução da entropia do sistema é dada pela entropia da sequência de medições,[18][24][25] que leva em consideração a redução da informação devido à correlação entre as medições.
Aplicações
editarVersões da vida real de demônios maxwellianos ocorrem, mas todos esses "demônios reais" ou demônios moleculares têm seus efeitos de redução de entropia devidamente equilibrados pelo aumento de entropia em outro lugar.[26] Mecanismos de tamanho molecular não são mais encontrados apenas na biologia; eles também são o assunto do campo emergente da nanotecnologia. Armadilhas de átomo único usadas por físicos de partículas permitem que um experimentador controle o estado de quanta individuais de uma forma semelhante ao demônio de Maxwell.
Se a hipotética matéria-espelho existir, Zurab Silagadze propõe que demônios podem ser previstos, "que podem agir como perpétuos móveis do segundo tipo: extrair energia térmica de apenas um reservatório, usá-la para fazer trabalho e ser isolado do resto do mundo comum. No entanto, a Segunda Lei não é violada porque os demônios pagam seu custo de entropia no setor oculto (espelho) do mundo emitindo fótons-espelho."[27]
Trabalho experimental
editarEm 2007, David Leigh anunciou a criação de um nanodispositivo baseado na catraca browniana popularizada por Richard Feynman. O dispositivo de Leigh é capaz de tirar um sistema químico do equilíbrio, mas deve ser alimentado por uma fonte externa (luz neste caso) e, portanto, não viola a termodinâmica.[28]
Anteriormente, pesquisadores incluindo o ganhador do Prêmio Nobel Fraser Stoddart criaram moléculas em forma de anel chamadas rotaxanos que poderiam ser colocadas em um eixo conectando dois locais, A e B. Partículas de qualquer local colidiriam com o anel e o moveriam de ponta a ponta. Se uma grande coleção desses dispositivos fosse colocada em um sistema, metade dos dispositivos teria o anel no local A e metade no B, em qualquer momento dado no tempo.[29]
Leigh fez uma pequena alteração no eixo para que se uma luz fosse lançada sobre o dispositivo, o centro do eixo engrossasse, restringindo o movimento do anel. Ele impede que o anel se mova, no entanto, somente se estiver em A. Com o tempo, portanto, os anéis serão empurrados de B para A e ficarão presos lá, criando um desequilíbrio no sistema. Em seus experimentos, Leigh foi capaz de levar um pote de "bilhões desses dispositivos" de um equilíbrio de 50:50 para um desequilíbrio de 70:30 em poucos minutos.[30]
Em 2009, Mark G. Raizen desenvolveu uma técnica de resfriamento atômico a laser que realiza o processo que Maxwell imaginou de classificar átomos individuais em um gás em diferentes recipientes com base em sua energia.[6][31][32] O novo conceito é uma parede unidirecional para átomos ou moléculas que permite que eles se movam em uma direção, mas não voltem. A operação da parede unidirecional depende de um processo atômico e molecular irreversível de absorção de um fóton em um comprimento de onda específico, seguido por emissão espontânea para um estado interno diferente. O processo irreversível é acoplado a uma força conservadora criada por campos magnéticos e/ou luz. Raizen e colaboradores propuseram usar a parede unidirecional para reduzir a entropia de um conjunto de átomos. Paralelamente, Gonzalo Muga e Andreas Ruschhaupt desenvolveram independentemente um conceito semelhante. Seu "diodo atômico" não foi proposto para resfriamento, mas sim para regular o fluxo de átomos. O Grupo Raizen demonstrou resfriamento significativo de átomos com a parede unidirecional em uma série de experimentos em 2008. Posteriormente, a operação de uma parede unidirecional para átomos foi demonstrada por Daniel Steck e colaboradores mais tarde em 2008. Seu experimento foi baseado no esquema de 2005 para a parede unidirecional e não foi usado para resfriamento. O método de resfriamento realizado pelo Grupo Raizen foi chamado de "resfriamento de fóton único", porque apenas um fóton em média é necessário para levar um átomo a quase repouso. Isso contrasta com outras técnicas de resfriamento a laser que usam o momento do fóton e exigem uma transição de ciclo de dois níveis.
Em 2006, Raizen, Muga e Ruschhaupt mostraram em um artigo teórico que, à medida que cada átomo cruza a parede unidirecional, ele espalha um fóton, e informações são fornecidas sobre o ponto de virada e, portanto, a energia dessa partícula. O aumento de entropia do campo de radiação espalhado de um laser direcional em uma direção aleatória é exatamente equilibrado pela redução de entropia dos átomos à medida que eles são presos pela parede unidirecional.
Esta técnica é amplamente descrita como um "demônio de Maxwell" porque realiza o processo de Maxwell de criar uma diferença de temperatura ao classificar átomos de alta e baixa energia em diferentes recipientes. No entanto, os cientistas apontaram que ela não viola a segunda lei da termodinâmica,[6][33] não resulta em uma diminuição líquida na entropia,[6][33] e não pode ser usada para produzir energia útil. Isso ocorre porque o processo requer mais energia dos feixes de laser do que poderia ser produzida pela diferença de temperatura gerada. Os átomos absorvem fótons de baixa entropia do feixe de laser e os emitem em uma direção aleatória, aumentando assim a entropia do ambiente.[6][33]
Em 2014, Pekola et al. demonstraram uma realização experimental de uma máquina de Szilárd.[34][35] Apenas um ano depois e com base em uma proposta teórica anterior,[36] o mesmo grupo apresentou a primeira realização experimental de um demônio de Maxwell autônomo, que extrai informações microscópicas de um sistema e reduz sua entropia aplicando feedback. O demônio é baseado em dois dispositivos de elétron único acoplados capacitivamente, ambos integrados no mesmo circuito eletrônico. A operação do demônio é observada diretamente como uma queda de temperatura no sistema, com um aumento simultâneo de temperatura no demônio decorrente do custo termodinâmico de geração de informações mútuas.[37] Em 2016, Pekola et al. demonstraram uma prova de princípio de um demônio autônomo em circuitos de elétron único acoplados, mostrando uma maneira de resfriar elementos críticos em um circuito com informação como combustível.[38] Pekola et al. também propuseram que um circuito qubit simples, por exemplo, feito de um circuito supercondutor, poderia fornecer uma base para estudar uma máquina de Szilard quântica.[39]
Como metáfora
editarDaemons na computação, geralmente processos que rodam em servidores para responder aos usuários, são nomeados em homenagem ao demônio de Maxwell.[40]
O historiador Henry Brooks Adams, em seu manuscrito A Regra da Fase Aplicada à História, tentou usar o demônio de Maxwell como uma metáfora histórica, embora tenha entendido mal e aplicado mal o princípio original.[41] Adams interpretou a história como um processo em direção ao "equilíbrio", mas ele viu nações militaristas (ele sentiu a Alemanha preeminente nesta classe) como tendendo a reverter esse processo, um demônio de Maxwell da história. Adams fez muitas tentativas de responder às críticas de sua formulação de seus colegas científicos, mas o trabalho permaneceu incompleto em sua morte em 1918 e foi publicado postumamente.[42]
Ver também
editarReferências
editar- ↑ Cargill Gilston Knott (1911). «;;Quote from undated letter from Maxwell to Tait». Life and Scientific Work of Peter Guthrie Tait (em inglês). [S.l.]: Cambridge University Press. pp. 213–215
- ↑ a b Thomson, William (9 de abril de 1874). «Kinetic theory of the dissipation of energy». Nature (em inglês). 9 (232): 441–444. Bibcode:1874Natur...9..441T. doi:10.1038/009441c0
- ↑ Leff & Rex (2002), p. 370.
- ↑ «The sorting demon of Maxwell». Nature (em inglês). 20 (501). 126 páginas. 1879. Bibcode:1879Natur..20Q.126.. doi:10.1038/020126a0
- ↑ Weber, Alan S. (2000). Nineteenth Century Science: a Selection of Original Texts (em inglês). [S.l.]: Broadview Press. p. 300
- ↑ a b c d e f g h i j k Bennett, Charles H. (novembro de 1987). «Demons, Engines, and the Second Law» (PDF). Scientific American (em inglês). 257 (5): 108–116. Bibcode:1987SciAm.257e.108B. doi:10.1038/scientificamerican1187-108. Consultado em 13 de novembro de 2014. Arquivado do original (PDF) em 3 de dezembro de 2020
- ↑ Maxwell (1871), reimpresso em Leff & Rex (1990) na página 4.
- ↑ a b c d e Sagawa, Takahiro (2012). Thermodynamics of Information Processing in Small Systems (em inglês). [S.l.]: Springer Science and Business Media. pp. 9–14. ISBN 978-4431541677
- ↑ Bennett, Charles H.; Schumacher, Benjamin (agosto de 2011). «Maxwell's demons appear in the lab» (PDF). Nikkei Science (em inglês): 3–6. Consultado em 13 de novembro de 2014
- ↑ Szilard, Leo (1929). «Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen (On the reduction of entropy in a thermodynamic system by the intervention of intelligent beings)». Zeitschrift für Physik. 53 (11–12): 840–856. Bibcode:1929ZPhy...53..840S. doi:10.1007/bf01341281 citado em Bennett 1987. Tradução em inglês disponível como Documento TT F-16723 da NASA publicado em 1976
- ↑ Landauer, R. (1961). «Irreversibility and heat generation in the computing process» (PDF). IBM Journal of Research and Development (em inglês). 5 (3): 183–191. doi:10.1147/rd.53.0183. Consultado em 13 de novembro de 2014 reimpresso em Volume 44, Nº 1, Janeiro de 2000, página 261 Arquivado em 2016-03-03 no Wayback Machine
- ↑ Bennett, C. H. (1982). «The thermodynamics of computation—a review» (PDF). International Journal of Theoretical Physics (Submitted manuscript) (em inglês). 21 (12): 905–940. Bibcode:1982IJTP...21..905B. CiteSeerX 10.1.1.655.5610 . doi:10.1007/BF02084158. Consultado em 10 de dezembro de 2017. Arquivado do original (PDF) em 14 de outubro de 2014
- ↑ Ball, Philip (2012). «The unavoidable cost of computation revealed». Nature (em inglês). doi:10.1038/nature.2012.10186
- ↑ Binder, P.M. (2023). «The reversibility paradox: Role of the velocity reversal step». International Journal of Theoretical Physics (em inglês). 62 (9): 200. Bibcode:2023IJTP...62..200B. doi:10.1007/s10773-023-05458-x
- ↑ Earman, John; Norton, John D. (1998). «Exorcist XIV: The Wrath of Maxwell's Demon. Part I. From Maxwell to Szilard» (PDF). Studies in History and Philosophy of Modern Physics (em inglês). 29 (4). 435 páginas. Bibcode:1998SHPMP..29..435E. doi:10.1016/s1355-2198(98)00023-9 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Earman, John; Norton, John D. (1999). «Exorcist XIV: The Wrath of Maxwell's Demon. Part II. From Szilard to Landauer and Beyond» (PDF). Studies in History and Philosophy of Modern Physics (em inglês). 30 (1). 1 páginas. Bibcode:1999SHPMP..30....1E. doi:10.1016/s1355-2198(98)00026-4 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Bennett, Charles H. (2002–2003). «Notes on Landauer's principle, reversible computation, and Maxwell's demon». Studies in History and Philosophy of Modern Physics (em inglês). 34 (3): 501–510. Bibcode:2003SHPMP..34..501B. arXiv:physics/0210005 . doi:10.1016/S1355-2198(03)00039-X
- ↑ a b c Cao, F. J.; Feito, M. (10 de abril de 2009). «Thermodynamics of feedback controlled systems». Physical Review E (em inglês). 79 (4): 041118. Bibcode:2009PhRvE..79d1118C. ISSN 1539-3755. PMID 19518184. arXiv:0805.4824 . doi:10.1103/PhysRevE.79.041118
- ↑ Sagawa, Takahiro; Ueda, Masahito (26 de fevereiro de 2008). «Second Law of Thermodynamics with Discrete Quantum Feedback Control». Physical Review Letters (em inglês). 100 (8). 080403 páginas. Bibcode:2008PhRvL.100h0403S. PMID 18352605. arXiv:0710.0956 . doi:10.1103/PhysRevLett.100.080403
- ↑ Hugo Touchette; Seth Lloyd (2000). «Information-Theoretic Limits of Control». Physical Review Letters (em inglês). 84 (6): 1156–1159. Bibcode:2000PhRvL..84.1156T. PMID 11017467. arXiv:chao-dyn/9905039 . doi:10.1103/PhysRevLett.84.1156 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Takahiro Sagawa; Masahito Ueda (2010). «Generalized Jarzynski Equality under Nonequilibrium Feedback Control». Physical Review Letters (em inglês). 104 (9). 090602 páginas. Bibcode:2010PhRvL.104i0602S. PMID 20366975. arXiv:0907.4914 . doi:10.1103/PhysRevLett.104.090602 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Armen E Allahverdyan, Dominik Janzing and Guenter Mahler (2009). «Thermodynamic efficiency of information and heat flow». Journal of Statistical Mechanics: Theory and Experiment (em inglês). 2009 (9): P09011. Bibcode:2009JSMTE..09..011A. arXiv:0907.3320 . doi:10.1088/1742-5468/2009/09/P09011
- ↑ Naoto Shiraishi; Takahiro Sagawa (2015). «Fluctuation theorem for partially masked nonequilibrium dynamics». Physical Review E (em inglês). 91 (1). 012130 páginas. Bibcode:2015PhRvE..91a2130S. PMID 25679593. arXiv:1403.4018 . doi:10.1103/PhysRevE.91.012130 Verifique o valor de
|name-list-format=amp(ajuda) - ↑ Jarillo, Javier; Tangarife, Tomás; Cao, Francisco J. (22 de janeiro de 2016). «Efficiency at maximum power of a discrete feedback ratchet». Physical Review E (em inglês). 93 (1). 012142 páginas. Bibcode:2016PhRvE..93a2142J. PMID 26871058. doi:10.1103/PhysRevE.93.012142
- ↑ Ruiz-Pino, Natalia; Villarrubia-Moreno, Daniel; Prados, Antonio; Cao-García, Francisco J. (12 de setembro de 2023). «Information in feedback ratchets». Physical Review E (em inglês). 108 (3). 034112 páginas. Bibcode:2023PhRvE.108c4112R. PMID 37849167 Verifique
|pmid=(ajuda). arXiv:2303.16804 . doi:10.1103/PhysRevE.108.034112 - ↑ Loewenstein, Werner R. (29 de janeiro de 2013). Physics in mind : a quantum view of the brain (em inglês). New York: Basic Books. ISBN 9780465029846. OCLC 778420640
- ↑ Silagadze, Z. K (2007). «Maxwell's demon through the looking glass». Acta Physica Polonica B (em inglês). 38 (1): 101–126. Bibcode:2007AcPPB..38..101S. arXiv:physics/0608114
- ↑ Serreli, V; Lee, CF; Kay, ER; Leigh, DA (fevereiro de 2007). «A molecular information ratchet». Nature (em inglês). 445 (7127): 523–527. Bibcode:2007Natur.445..523S. PMID 17268466. doi:10.1038/nature05452
- ↑ Bissell, Richard A; Córdova, Emilio; Kaifer, Angel E.; Stoddart, J. Fraser (12 de maio de 1994). «A chemically and electrochemically switchable molecular shuttle». Nature (em inglês). 369 (6476): 133–137. Bibcode:1994Natur.369..133B. doi:10.1038/369133a0
- ↑ Katharine Sanderson (31 de janeiro de 2007). «A demon of a device». Nature (em inglês). doi:10.1038/news070129-10
- ↑ Raizen, Mark G. (12 de junho de 2009). «Comprehensive Control of Atomic Motion». Science (em inglês). 324 (5933): 1403–1406. Bibcode:2009Sci...324.1403R. PMID 19520950. doi:10.1126/science.1171506
- ↑ Raizen, Mark G. (março de 2011). «Demons, Entropy, and the Quest for Absolute Zero». Scientific American (em inglês). 304 (3): 54–59. Bibcode:2011SciAm.304c..54R. PMID 21438491. doi:10.1038/scientificamerican0311-54. Consultado em 14 de novembro de 2014
- ↑ a b c Orzel, Chad (25 de janeiro de 2010). «Single-Photon Cooling: Making Maxwell's Demon». Uncertain Principles (em inglês). ScienceBlogs (website). Consultado em 14 de novembro de 2014
- ↑ Koski, J.V.; Maisi, V.F.; Sagava, T.; Pekola, J.P. (14 de julho de 2014). «Experimental Observation of the Role of Mutual Information in the Nonequilibrium Dynamics of a Maxwell Demon». Physical Review Letters (em inglês). 113 (3): 030601. Bibcode:2014PhRvL.113c0601K. PMID 25083623. arXiv:1405.1272 . doi:10.1103/PhysRevLett.113.030601
- ↑ Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. (23 de setembro de 2014). «Experimental realization of a Szilard engine with a single electron». Proceedings of the National Academy of Sciences of the United States of America (em inglês). 111 (38): 13786–9. Bibcode:2014PNAS..11113786K. PMC 4183300 . PMID 25201966. arXiv:1402.5907 . doi:10.1073/pnas.1406966111
- ↑ Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. (24 de janeiro de 2013). «Thermodynamics of a Physical Model Implementing a Maxwell Demon». Physical Review Letters (Submitted manuscript) (em inglês). 110 (4): 040601. Bibcode:2013PhRvL.110d0601S. PMID 25166147. arXiv:1210.5661 . doi:10.1103/PhysRevLett.110.040601
- ↑ Koski, J.V.; Kutvonen, A.; Khaymovich, I.M.; Ala-Nissila, T.; Pekola, J.P. (2015). «On-Chip Maxwell's Demon as an Information-Powered Refrigerator». Physical Review Letters (em inglês). 115 (26): 260602. Bibcode:2015PhRvL.115z0602K. PMID 26764980. arXiv:1507.00530 . doi:10.1103/PhysRevLett.115.260602
- ↑ Koski, J.V.; Pekola, J.P. (16 de dezembro de 2016). «Maxwell's demons realized in electronic circuits». Comptes Rendus Physique (em inglês). 17 (10): 1130–1138. Bibcode:2016CRPhy..17.1130K. doi:10.1016/j.crhy.2016.08.011
- ↑ Pekola, J.P.; Golubev, D.S.; Averin, D.V. (5 de janeiro de 2016). «Maxwell's demon based on a single qubit». Physical Review B (em inglês). 93 (2): 024501. Bibcode:2016PhRvB..93b4501P. arXiv:1508.03803 . doi:10.1103/PhysRevB.93.024501
- ↑ Fernando J. Corbató (23 de janeiro de 2002). «Take Our Word for It» (em inglês). Consultado em 20 de agosto de 2006
- ↑ Cater (1947), pp. 640–647; ver também Daub (1970), reimpresso em Leff & Rex (1990), páginas 37–51.
- ↑ Adams (1919), página 267.
Bibliografia
editar- Cater, H. D., ed. (1947). Henry Adams and his Friends (em inglês). [S.l.]: Boston
- Daub, E. E. (1967). «Atomism and Thermodynamics». Isis (em inglês). 58 (3): 293–303. doi:10.1086/350264
- Leff, Harvey S. & Andrew F. Rex, ed. (1990). Maxwell's Demon: Entropy, Information, Computing (em inglês). Bristol: Adam-Hilger. ISBN 978-0-7503-0057-5
- Leff, Harvey S. & Andrew F. Rex, ed. (2002). Maxwell's Demon 2: Entropy, Classical and Quantum Information, Computing (em inglês). [S.l.]: CRC Press. ISBN 978-0-7503-0759-8
- Adams, H. (1919). The Degradation of the Democratic Dogma (em inglês). New York: Kessinger. ISBN 978-1-4179-1598-9