Distância de Hamming

Na teoria da informação, a distância de Hamming entre duas strings de mesmo comprimento é o número de posições nas quais elas diferem entre si. Vista de outra forma, ela corresponde ao menor número de substituições necessárias para transformar uma string na outra, ou o número de erros que transformaram uma na outra.

cubo binário de 3 bits para determinar a distância de Hamming	Dois exemplos desta distância: 100->011 tem distância 3 (caminho vermelho); 010->111 tem distância 2 (caminho azul)
hipercubo cubo binário de 4 bits para determinar a distância de Hamming
Dois exemplos desta distância: 0100->1001 tem distância 3 (caminho vermelho); 0110->1110 tem distância 1 (caminho azul)

História e aplicações

A distância de Hamming é assim chamada em homenagem a Richard Hamming, que introduziu o conceito em um artigo fundamental sobre códigos de Hamming Error detecting and error correcting codes em 1950.^[1] Nas telecomunicações, ela é utilizada para sinalizar erros na transmissão de palavras binárias de comprimento fixo entre um emissor e um receptor, e por isso é algumas vezes chamada de "distância do sinal". Esta forma de análise de bits é usada em várias disciplinas incluindo a teoria da informação, a teoria de códigos e a criptografia. No entanto, para comparar strings de tamanhos diferentes, ou nas quais não apenas substituições mas também inserções e remoções devem ser esperadas, é mais apropriado usar uma métrica mais sofisticada como a distância de Levenshtein.

Para strings q-árias sobre um alfabeto de tamanho q ≥ 2 a distância de Hamming é aplicada no caso da modulação ortogonal, enquanto a distância de Lee é usada para modulação de fase. Se q = 2 ou q = 3 ambas as distâncias coincidem

A distância de Hamming também é usada em sistemática como uma medida da distância genética.^[2]

Em uma grade (tal como um tabuleiro de xadrez), os pontos a uma distância de Lee de 1 unidade constituem uma vizinhança de Von Neumann de tal ponto.

Propriedades especiais

Para um comprimento n fixado, a distância de Hamming é uma métrica no espaço vetorial das palavras daquele comprimento, uma vez que ela obviamente cumpre as condições de ser não negativa, de distinguir apenas palavras que sejam distintas e de simetria, e pode-se mostrar facilmente por indução completa que ela também verifica a desigualdade triangular. A distância de Hamming entre duas palavras a e b também pode ser vista como o peso de Hamming de a − b escolhendo-se o operador − adequadamente.

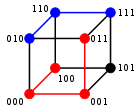
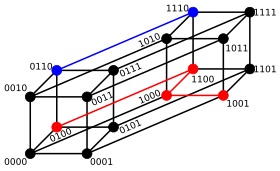
Para strings binárias a e b, a distância de Hamming é igual ao número de uns em a XOR b. O espaço métrico das strings binárias de comprimento n, com a métrica de Hamming é conhecido como cubo de Hamming; ele é equivalente como espaço métrico ao conjunto das distâncias entre vértices em um grafo hipercubo. Também é possível interpretar uma string binária de comprimento n como um vetor em $R^{n}$ tratando cada símbolo da string como uma coordenada real; com essa imersão, as strings formam os vértices de um hipercubo de dimensão n, e a distância de Hamming entre as strings é equivalente à métrica do taxi entre os vértices.

Exemplos

A distância de Hamming entre:

"elabore" e "melhore" é 4.
2173896 e 2233796 é 3.
11011 e 10011 é 1.

Neste terceiro exemplo, se a cadeia de bits A(11011) fosse emitida e chegasse ao receptor como A'(10011), poderia ser usada a operação XOR da seguinte maneira:

11011

XOR 10011

01000

A quantidade de bits encontrados nessa operação, é a Distância de Hamming entre a palavra transmitida e a recebida. Deste modo, conclui-se que a distância de Hamming entre as strings do exemplo é 1, pois apenas 1 bit foi encontrado após a operação XOR.

Usa-se normalmente esta teoria nos mapas de Karnaugh, servindo para simplificar expressões algébricas usadas para a construção de circuitos.

Algoritmo de exemplo

A função Python hamming_distance() calcula a distância de Hamming entre duas strings (ou outros objetos iteráveis) de mesmo comprimento, criando uma sequência de a zeros e uns indicando diferenças e correspondências entre as posições correspondentes das duas entradas, e então somando a sequência.

Python

def hamming_distance(s1, s2):
    assert len(s1) == len(s2)
    return sum(ch1 != ch2 for ch1, ch2 in zip(s1, s2))

A seguinte função C calculará a distância de Hamming entre dois inteiros (considerados como valores binários, isto é, como sequências de zeros e uns). O tempo de execução deste procedimento é proporcional à distância de Hamming em vez do número de bits nas entradas. Ela calcula o ou exclusivo bit a bit entre as duas entradas, e então determina o peso de Hamming do resultado (o número de bits não nulos) usando um algoritmo de Wegner (1960) que repetidamente procura e limpa o bit não nulo de menor ordem.

C

unsigned hamdist(unsigned x, unsigned y)
{
  unsigned dist = 0, val = x ^ y;

  // Count the number of set bits
  while(val)
  {
    ++dist;
    val &= val - 1;
  }

  return dist;
}

Matlab / Octave

function [dist] = hamdist(x, y)
    dist = x ~= y;
end

Ver também

Notas

↑ Hamming (1950).
↑ Pilcher, Wong & Pillai (2008).

Referências

O artigo em inglês, a partir do qual parte deste foi traduzido, incorporava material em domínio público do documento da Administração dos Serviços Gerais "Federal Standard 1037C".
Hamming, Richard W. (1950), «Error detecting and error correcting codes» 🔗 (PDF), Bell System Technical Journal, 29 (2): 147–160, MR 0035935, consultado em 11 de outubro de 2010, cópia arquivada (PDF) em 25 de maio de 2006
HEFEZ, Abramo; VILLELA, Maria Lúcia T. (2002). Códigos Corretores de Erros. Rio de Janeiro: IMPA
Pilcher, C. D.; Wong, J. K.; Pillai, S. K. (março de 2008), «Inferring HIV transmission dynamics from phylogenetic sequence relationships», PLoS Med., 5 (3): e69, PMC 2267810 , PMID 18351799, doi:10.1371/journal.pmed.0050069 .
Roman, Steven (1997). Introduction to Coding and Information Theory. [S.l.]: Springer. ISBN 0-387-94704-3
Tanenbaum, Andrew S.. Redes de Computadores. 4ªEd. Ed. Elsevier
Wegner, Peter (1960), «A technique for counting ones in a binary computer», Communications of the ACM, 3 (5): 322, doi:10.1145/367236.367286

Ligações externas

Exemplo de distância de Hamming (em inglês)
Hamming Code Tool Ferramenta para gerar códigos de Hamming
set_matcher Ferramenta para comparar duas famílias de conjuntos a partir da mesma população base usando a distância de Hamming.

[1] Hamming (1950).

[pmid18351799-2] Pilcher, Wong & Pillai (2008).

[1]

[2]