Ficheiro:SpaceBattle.png
SpaceBattle.png (306 × 301 píxeis, tamanho: 12 kB, tipo MIME: image/png)
|
|
Esta imagem provém do Wikimedia Commons, um acervo de conteúdo livre da Wikimedia Foundation que pode ser utilizado por outros projetos.
|
Descrição do ficheiro
| DescriçãoSpaceBattle.png |
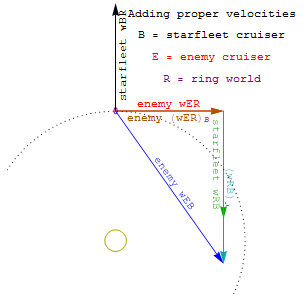
English: A starfleet battle-cruiser drops out of hyperspace in the orbital plane of a ringworld, traveling at 1 ly/ty radially away from the ringworld's star. An enemy cruiser drops out of hyperspace nearby at the same time, traveling 1 ly/ty in the rotation-direction of the ringworld's orbit, and in a direction perpendicular to the starfleet cruiser's radial-trajectory .
What is the proper-velocity (magnitude and direction) of the enemy cruiser relative to the starfleet ship? |
||
| Data | |||
| Origem | Obra do próprio | ||
| Autor | P. Fraundorf | ||
| Outras versões |
|
Added information

As pointed out here[1], local momenta per unit mass or proper-velocities w ≡ dx/dτ add as 3-vectors (in analogy to the classical expression vAC = vAB+vBC), provided that we re-scale/direct the "out-of-frame" component wAB and time-dilate wBC according to:
where the first term is the non-proper "shared clock but not metric" velocity:
while the second term is the non-proper "shared metric but not clock" velocity:
.
One consequence of this is that wCA (which uses A's rather than C's definition of simultaneity) will have the same magnitude as, but a different direction than, wAC. Because the gamma factors are always greater than one, it is easy to see from the equation that the proper-velocity sum direction will be "Thomas-precessed" from wAB+wBC toward the direction of the intermediate frame's proper-velocity wBC.
- Note that we've now corrected the figure (and equations above) for a "Thomas-precession" rotation error in the solution above. A correction to the code listed below is also in the works. Unitsphere (discussão) 18:06, 20 July 2017 (UTC)

Coordinate-velocity 3-vectors do not similarly add. Also of course proper-velocity is proportional to momentum in the map-frame, while both proper-time (and proper-acceleration as needed in this context) are frame invariants.
This makes 3-vector velocities and accelerations much more useful at high-speeds in the traveler-kinematic[2] (using proper-time τ, proper-velocity w ≡ dx/dτ and proper-acceleration α) than in the Galilean-kinematic[3] (using map-time t, coordinate-velocity v ≡ dx/dt and coordinate-acceleration a ≡ dv/dt).
Aside: Note that the orbiting ringworld depicted above is more like those in Bungie corporation's Halo universe, than the immense concentric structure described in Larry Niven's ringworld universe.
A challenging follow-on to this might be to ask how long it would take to catch up to and dock with the enemy, assuming that its speed and direction are fixed, while your ship is capable of 1-gee acceleration. Any volunteers?
Code
Some useful Mathematica 8.0 declarations for use with two or three-vector arguments, regardless of the speeds and directions involved, include:
gammaw[w_] := Sqrt[1 + w.w] wABbyCn[wAB_, wBC_] := wAB + (gammaw[wBC] - 1) wAB.wBC/wBC.wBC wBC
wBCbyCn[wAB_, wBC_] := gammaw[wAB] wBC
wACbyCn[wAB_, wBC_] := wABbyCn[wAB, wBC] + wBCbyCn[wAB, wBC]
Here we set up the problem by specifying (in lightspeed units) the proper-velocity vectors of the starfleet battle-cruiser B with respect to the ring (R), and of the enemy battle-cruiser (E) with respect to the ring. Finally, we specify the xy coordinates of the ring relative to its own star in the diagram:
wBR = {0, 1}; wER = {1, 0}; halo = {0, 1.2};
Answers:
enemyProperSpeedEB = Norm[wACbyCn[wER, -wBR]]
This yields wEB = Sqrt[3] in units of ly/ty.
enemyDirectionEB = ArcTan[wACbyCn[wER, -wBR]1, wACbyCn[wER, -wBR]2]*180./Pi
This puts the angle at -54.7356 degrees.
The plot is might be made by the following command:
Graphics[
{
Darker[Yellow], Circle[{0, 0}, .1],
Purple, Circle[halo, {.015, .03}],
Black,
Arrow[{halo, halo + wBR}],
Text["bship wBR", halo + wBR/2, {0, -1}, -wBR],
Red,
Text["enemy wER", halo + wER/2, {0, -1}, wER],
Arrow[{halo, halo + wER}],
Blue,
Arrow[{halo, halo + wACbyCn[wER, -wBR]}],
Text["enemy wEB",
halo + wACbyCn[wER, -wBR]/2, {0, -1}, {wACbyCn[wER, -wBR][[1]],
wACbyCn[wER, -wBR][[2]]}],
Darker[Green],
Arrow[{halo(*+wABbyCn[wER,-wBR]*),
halo(*+wABbyCn[wER,-wBR]*)- wBR}],
Text["ring wRB", halo(*+wABbyCn[wER,-wBR]*)- wBR/2, {0, 1}, -wBR],
Gray,
Dashed,
Line[{halo, halo + wABwithBtoC, halo + wAC, halo + wBCwithBtoA,
halo}],
Darker[Cyan],
Arrow[{halo + wABbyCn[wER, -wBR],
halo + wBCbyCn[wER, -wBR] + wABbyCn[wER, -wBR]}],
Text["ring (wRB)R\[Rule]E",
halo + wABbyCn[wER, -wBR] + wBCbyCn[wER, -wBR]/2, {0, -1},
wBCbyCn[wER, -wBR]],
Darker[Orange],
Arrow[{halo, halo + wABbyCn[wER, -wBR]}],
Text["enemy (wER)R\[Rule]B", halo + wABbyCn[wER, -wBR]/2, {0, 1},
wABbyCn[wER, -wBR]],
Black, Dotted,
Circle[{0, 0}, Norm[halo]],
Text["Find wEB from wER and wRB", labelHigh(*{.9,3.0}*)],
Text["B = starfleet battleship", labelHigh - {0, 0.2}],
Red, Text["E = enemy cruiser", labelHigh - {0, 0.4}],
Purple, Text["R = ring world", labelHigh - {0, 0.6}]
},
PlotRange -> pRange(*{{-1,2},{-.5,2.5}}*),
BaseStyle -> {FontFamily -> "Courier", FontSize -> 12}
]
Footnotes
- ↑ P. Fraundorf (2016/2017) Traveler-point dynamics, hal-01503971 working draft on-line discussion.
- ↑ P. Fraundorf (2012) "A traveler-centered intro to kinematics", arxiv:1206.2877 [physics.pop-ph].
- ↑ Anthony P. French (1968) Special relativity (W. W. Norton, NY) page 154: "...acceleration is a quantity of limited and questionable value in special relativity."
Licenciamento
- Pode:
- partilhar – copiar, distribuir e transmitir a obra
- recombinar – criar obras derivadas
- De acordo com as seguintes condições:
- atribuição – Tem de fazer a devida atribuição da autoria, fornecer uma hiperligação para a licença e indicar se foram feitas alterações. Pode fazê-lo de qualquer forma razoável, mas não de forma a sugerir que o licenciador o apoia ou subscreve o seu uso da obra.
- partilha nos termos da mesma licença – Se remisturar, transformar ou ampliar o conteúdo, tem de distribuir as suas contribuições com a mesma licença ou uma licença compatível com a original.
Legendas
Elementos retratados neste ficheiro
retrata
Um valor sem um elemento no repositório Wikidata
17 fevereiro 2014
Histórico do ficheiro
Clique uma data e hora para ver o ficheiro tal como ele se encontrava nessa altura.
| Data e hora | Miniatura | Dimensões | Utilizador | Comentário | |
|---|---|---|---|---|---|
| atual | 18h03min de 20 de julho de 2017 |  | 306 × 301 (12 kB) | Unitsphere | Corrected a "Thomas precession" rotation error in the intial version of this solution. |
| 16h50min de 17 de fevereiro de 2014 |  | 398 × 331 (9 kB) | Unitsphere | User created page with UploadWizard |
Utilização local do ficheiro
A seguinte página usa este ficheiro:
Utilização global do ficheiro
As seguintes wikis usam este ficheiro:
- ca.wikipedia.org
- en.wikipedia.org
Metadados
Este ficheiro contém informação adicional, provavelmente adicionada a partir da câmara digital ou scanner utilizada para criar ou digitalizar a imagem. Caso o ficheiro tenha sido modificado a partir do seu estado original, alguns detalhes poderão não refletir completamente as mudanças efetuadas.
| Resolução horizontal | 37,79 pt/cm |
|---|---|
| Resolução vertical | 37,79 pt/cm |
| Data e hora de digitalização |
|