Na matemática , funções hiperbólicas são funções análogas às funções trigonométricas ordinárias, estas também conhecidas como funções circulares. Funções hiperbólicas foram introduzidas por volta de 1760 de maneira independente pelos matemáticos Vincenzo Riccati e Johann Heinrich Lambert [ 1] funções hiperbólicas básicas são o seno hiperbólico e o cosseno hiperbólico , dos quais são derivados a tangente hiperbólica , a cossecante hiperbólica ou a secante hiperbólica e a cotangente hiperbólica , análogas às funções trigonométricas derivadas . Em alguns casos, suas inversas também são consideradas funções hiperbólicas.
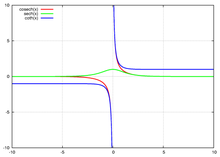
O seno, cosseno e tangente hiperbólicos. A cossecante, a secante e a cotangente hiperbólicas. Essa classe de funções recebe esse nome porque, em muitos casos nos quais o uso de funções trigonométricas gera círculos ou elipses , o uso de funções hiperbólicas gera hipérboles , como, por exemplo, no caso das equações paramétricas :
x
=
cos
t
{\displaystyle x=\cos t\,}
y
=
sin
t
{\displaystyle y=\sin t\,}
Estas geram um círculo , enquanto que as equações:
x
=
cosh
t
{\displaystyle x=\cosh t\,}
y
=
sinh
t
{\displaystyle y=\sinh t\,}
geram (uma metade de) uma hipérbole .
Funções hiperbólicas aparecem nas soluções de várias equações diferenciais lineares, nas soluções de algumas equações cúbicas , em cálculos de ângulos e distâncias na geometria hiperbólica e em cálculos da Equação de Laplace em coordenadas cartesianas . Equações de Laplace são importantes em diversas áreas da física , incluindo eletromagnetismo , transferência de calor , hidrodinâmica e relatividade restrita .
Na análise complexa , as funções hiperbólicas surgem como as partes imaginárias das funções trigonométricas seno e cosseno . Quando são consideradas como definidas por uma variável complexa, as funções hiperbólicas são funções racionais de exponenciais e, portanto, holomórficas .
editar
As expressões das funções hiperbólicas são as seguintes:
sinh
x
=
e
x
−
e
−
x
2
=
e
2
x
−
1
2
e
x
=
1
−
e
−
2
x
2
e
−
x
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}}
cosh
x
=
e
x
+
e
−
x
2
=
e
2
x
+
1
2
e
x
=
1
+
e
−
2
x
2
e
−
x
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}}
tanh
x
=
sinh
x
cosh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
{\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}
=
e
2
x
−
1
e
2
x
+
1
=
1
−
e
−
2
x
1
+
e
−
2
x
{\displaystyle ={\frac {e^{2x}-1}{e^{2x}+1}}={\frac {1-e^{-2x}}{1+e^{-2x}}}}
Cotangente hiperbólica:
x
≠
0
{\displaystyle x\not =0}
coth
x
=
cosh
x
sinh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
{\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=}
=
e
2
x
+
1
e
2
x
−
1
=
1
+
e
−
2
x
1
−
e
−
2
x
{\displaystyle ={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}}}
sech
x
=
1
cosh
x
=
2
e
x
+
e
−
x
{\displaystyle \operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}}
=
2
e
x
e
2
x
+
1
=
2
e
−
x
1
+
e
−
2
x
{\displaystyle ={\frac {2e^{x}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}}
Cossecante hiperbólica:
x
≠
0
{\displaystyle x\not =0}
csch
x
=
1
sinh
x
=
2
e
x
−
e
−
x
{\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}}
=
2
e
x
e
2
x
−
1
=
2
e
−
x
1
−
e
−
2
x
{\displaystyle ={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}}}
editar
As derivadas das funções hiperbólicas são as seguintes:
Derivada do seno hiperbólico:
d
d
x
sinh
x
=
cosh
x
{\displaystyle {\frac {d}{dx}}\sinh x=\cosh x}
Derivada do cosseno hiperbólico:
d
d
x
cosh
x
=
sinh
x
{\displaystyle {\frac {d}{dx}}\cosh x=\sinh x}
Derivada da tangente hiperbólica:
d
d
x
tanh
x
=
1
−
tanh
2
x
=
sech
2
x
=
1
/
cosh
2
x
{\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x=\operatorname {sech} ^{2}x=1/\cosh ^{2}x}
Derivada da cotangente hiperbólica:
d
d
x
coth
x
=
1
−
coth
2
x
=
−
csch
2
x
=
−
1
/
sinh
2
x
{\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-1/\sinh ^{2}x}
x
≠
0
{\displaystyle x\not =0}
Derivada da secante hiperbólica:
d
d
x
sech
x
=
−
tanh
x
sech
{\displaystyle {\frac {d}{dx}}\ \operatorname {sech} \,x=-\tanh x\ \operatorname {sech} }
Derivada da cossecante hiperbólica:
d
d
x
csch
x
=
−
coth
x
csch
{\displaystyle {\frac {d}{dx}}\ \operatorname {csch} \,x=-\coth x\ \operatorname {csch} }
x
≠
0
{\displaystyle x\not =0}
editar
Ver artigo principal: Função hiperbólica inversa
As derivadas das funções hiperbólicas inversas (também chamadas de funções arco) são as seguintes:
d
d
x
arsinh
x
=
1
x
2
+
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}
Derivada do arco cosseno hiperbólico:
d
d
x
arcosh
x
=
1
x
2
−
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}
1
<
x
{\displaystyle 1<x}
Derivada do arco tangente hiperbólico:
d
d
x
artanh
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}
−
1
<
x
<
1
{\displaystyle -1<x<1}
Derivada do arco cotangente hiperbólico:
d
d
x
arcoth
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}
|
x
|
>
1
{\displaystyle \left\vert x\right\vert >1}
Derivada do arco secante hiperbólico:
d
d
x
arsech
x
=
−
1
x
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}
0
<
x
<
1
{\displaystyle 0<x<1}
Derivada do arco cossecante hiperbólico:
d
d
x
arcsch
x
=
−
1
|
x
|
1
+
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}}
x
≠
0
{\displaystyle x\not =0}
editar
As funções hiperbólicas podem ser definidas, usando-se números complexos , a partir das funções trigonométricas:
sin
(
i
x
)
=
i
sinh
x
{\displaystyle \sin(ix)=i\sinh x\,}
cos
(
i
x
)
=
cosh
x
{\displaystyle \cos(ix)=\cosh x\,}
tan
(
i
x
)
=
i
tanh
x
{\displaystyle \tan(ix)=i\tanh x\,}
cos
(
x
)
=
cosh
(
i
x
)
{\displaystyle \cos(x)=\cosh(ix)}
sin
(
x
)
=
i
sinh
(
−
i
x
)
{\displaystyle \sin(x)=i\sinh(-ix)}
tan
(
x
)
=
i
tanh
(
−
i
x
)
{\displaystyle \tan(x)=i\tanh(-ix)\,}
onde i é uma unidade imaginária com a propriedade i 2 = −1.
As formas complexas nas definições acima são provenientes da Fórmula de Euler .
Prova resumida de
cos
(
i
x
)
=
cosh
(
x
)
{\displaystyle \cos(ix)=\cosh(x)}
cos
(
x
y
)
=
e
x
y
i
1
2
+
e
−
x
y
i
1
2
{\displaystyle \cos(xy)=e^{xyi}{\frac {1}{2}}+e^{-xyi}{\frac {1}{2}}}
cos
(
i
x
)
=
e
−
x
1
2
+
e
x
1
2
=
cosh
(
x
)
{\displaystyle \cos(ix)=e^{-x}{\frac {1}{2}}+e^{x}{\frac {1}{2}}=\cosh(x)}
O mesmo funciona para as demais relações afirmadas.
editar
(
senh
(
t
)
+
cosh
(
t
)
)
m
=
(
e
t
)
m
=
e
m
t
=
senh
(
m
t
)
+
cosh
(
m
t
)
{\displaystyle (\operatorname {senh} (t)+\cosh(t))^{m}=(e^{t})^{m}=e^{mt}=\operatorname {senh} (mt)+\cosh(mt)}
e
2
t
=
(
sinh
(
t
)
+
cosh
(
t
)
cosh
(
t
)
−
sinh
(
t
)
)
{\displaystyle e^{2t}=\left({\frac {\sinh(t)+\cosh(t)}{\cosh(t)-\sinh(t)}}\right)}
e
2
t
=
(
sinh
(
t
)
+
cosh
(
t
)
)
2
{\displaystyle e^{2t}=(\sinh(t)+\cosh(t))^{2}}
cosh
2
(
t
)
−
senh
2
(
t
)
=
1
{\displaystyle \cosh ^{2}(t)-\operatorname {senh} ^{2}(t)=1}
e
−
t
(
sinh
(
t
)
+
cosh
(
t
)
)
=
1
{\displaystyle e^{-t}(\sinh(t)+\cosh(t))=1}
e
t
(
sinh
(
t
)
−
cosh
(
t
)
)
=
−
1
{\displaystyle e^{t}(\sinh(t)-\cosh(t))=-1}
↑ Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Página 100.
- GRAVILLE SMITH, William Elementos de Cálculo Diferencial e Integral Editora Biblioteca da Marinha do Brasil , 1950.
Catenária , o gráfico da função
y
=
cosh
x
{\displaystyle y=\cosh x\,}