Grade cartesiana

Uma grade regular é uma tesselação de um Espaço euclidiano de n dimensões criado por paralelepípedos. Grades desse tipo aparecem em papéis milimetrados e podem ser usados em Método dos elementos finitos, assim como em Método dos volumes finitos e em Método das diferenças finitas. Como as derivadas de campo são expressas convenientemente como diferenças finitas, grades estruturadas aparecem muito em métodos de diferença finita. Grades desestruturadas oferecem mais flexibilidade que grades estruturadas e, por isso, são mais úteis em métodos de volume e elementos finitos.

Exemplo de uma grade cartesiana.

Exemplo de uma grade regular.

Exemplo de uma grade retilinear.

Exemplo de uma grade curvilinear.

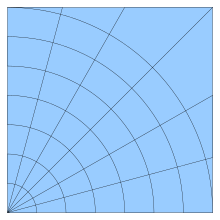
Cada célula na grade pode ser endereçada pelo índice em duas (i,j) ou três (i,j,k) dimensões, e cada vértice tem coordenadas $(i\cdot dx,j\cdot dy)$ em 2D ou $(i\cdot dx,j\cdot dy,k\cdot dz)$ em 3D para algum número real dx, dy e dz representando o espaço da grade.

Grades relacionadas

Uma Grade cartesiana é um caso especial onde os elementos são quadrados unitários ou cubos unitários e os vértices são pontos inteiros.

Uma Grade retilinear é uma tesselação de retângulos ou paralelepípedos que não são, em geral, todos congruentes. As células ainda podem ser indexadas por inteiros, como na grade cartesiana, mas o mapeamento de índices para coordenadas de vértices é menos uniforme que uma grade regular.

Uma Grade curvilinear ou Grade estruturada é uma grade que possui a mesma estrutura de uma grade regular, onde as células são quadriláteras ou cúbicas, ao invés de relangulos e paralelepípedos retangulares.

Ver também

• Sistemas de coordenadas cartesianos
• Grade de inteiros (página em inglês)
• Grade desestruturada (página em inglês)

Notas

• Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Regular Grid».