Grafo de Shrikhande
No campo da matemática da teoria dos grafos, o Grafo de Shrikhande é um grafo nomeado descoberto por S. S. Shrikhande em 1959.[1] é um grafo fortemente regular com 16 vértices e 48 arestas, com cada vértice tendo um grau de 6.
| Grafo de Shrikhande | |
|---|---|
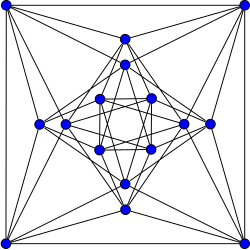
| |
| Nomeado em honra a | S. S. Shrikhande |
| vértices | 16 |
| arestas | 48 |
| Raio | 2 |
| Diâmetro | 2 |
| Cintura | 3 |
| Automorfismos | 192 |
| Número cromático | 4 |
| Índice cromático | 6 |
| Propriedades | Simétrico Euleriano Hamiltoniano Integral Fortemente regular |
Propriedades
editarNo grafo de Shrikhande, quaisquer dois vértices I e J têm dois vizinhos distintos em comum (excluindo os próprios dois vértices I e J), o que é verdade independentemente de I ser adjacente a J. Em outras palavras, seus parâmetros para ser fortemente regulares são: {16,6,2,2}, com , esta igualdade implicando que o grafo é associado a um BIBD simétrico. Ele compartilha esses parâmetros com um grafo diferente, o 4×4 grafo torre (rook's graph).
O grafo de Shrikhande é localmente hexagonal; isto é, os vizinhos de cada vértice formam um grafo ciclo de seis vértices. Como em qualquer grafo localmente cíclico, o grafo de Shrikhande é o 1-esqueleto de uma triangulação de Whitney de alguma superfície; no caso do grafo de Shrikhande, esta superfície é um toro em que cada vértice é cercado por seis triângulos.[2] Assim, o grafo de Shrikhande é um grafo toroidal. O dual desta incorporação é o grafo de Dick, um grafo cúbico simétrico.
O grafo de Shrikhande não é um grafo distância-transitivo. É o menor grafo distância-regular que não é a distância-transitivo.[3]
O grupo de automorfismo do grafo de Shrikhande é da ordem de 192. Ele age transitivamente sobre os vértices, nas arestas e nos arcos do grafo.
O polinômio característico do grafo de Shrikhande é: . Portanto o grafo de Shrikhande é um grafo integral: seu espectro consiste inteiramente de inteiros.
Referências
- ↑ SHRIKHANDE, S. S. (1959). «The uniqueness of the L2 association scheme». Annals of Mathematical Statistics. 30. pp. 781–798.
- ↑ BROUWER, A. E. «Shrikhande graph». Consultado em 10 de novembro de 2010.
- ↑ BROUWER, A. E.; COHEN, A. M.; NEUMAIER, A. (1989). Distance-Regular Graphs. New York: Springer-Verlag. pp. 104–105 e 136. ISBN 0387506195 ISBN 978-0387506197.
Ligações externas
editar- «O grafo de Shrikhande». , Peter Cameron, Agosto de 2010.
Galeria
editar-
O grafo de Shrikhande é um grafo toroidal.
-
O número cromático do grafo de Shrikhande é 4.
-
O índice cromático do grafo de Shrikhande é 6.
-
O grafo de Shrikhande desenhado simetricamente.
-
O grafo de Shrikhande é Hamiltoniano.