Sistema cristalino hexagonal
O sistema cristalino hexagonal é uma das seis famílias de cristais, que inclui dois sistemas de cristais (hexagonal e trigonal) e dois sistemas de rede (hexagonal e romboédrico). Embora comumente confundidos, o sistema cristalino trigonal e o sistema de rede romboédrica não são equivalentes. Em particular, existem cristais que têm simetria trigonal, mas pertencem à rede hexagonal (como o α-quartzo).[1]
A família de cristais hexagonais consiste nos 12 grupos de pontos, de modo que pelo menos um de seus grupos espaciais tem a rede hexagonal como rede subjacente e é a união do sistema cristalino hexagonal e do sistema cristalino trigonal. Existem 52 grupos espaciais associados a ele, que são exatamente aqueles cuja rede de Bravais é hexagonal ou romboédrica.[2]
Sistemas de treliça
editarA família de cristais hexagonais consiste em dois sistemas de rede: hexagonal e romboédrico. Cada sistema de rede consiste em uma rede de Bravais.
| Malha de Bravais | Hexagonal | Romboédrico |
|---|---|---|
| Símbolo de Pearson | hP | hR |
| Célula unitária hexagonal | ||
| Célula unitária romboédrica |
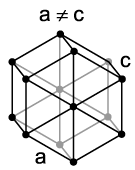
Na família hexagonal, o cristal é convencionalmente descrito por uma célula unitária de prisma rômbico reto com dois eixos iguais (a por a), um ângulo incluído de 120° (γ) e uma altura (c, que pode ser diferente de a) perpendicular aos dois eixos de base.[3]
A célula unitária hexagonal para a rede romboédrica de Bravais é a célula centrada em R, consistindo em dois pontos de rede adicionais que ocupam uma diagonal do corpo da célula unitária. Existem duas maneiras de fazer isso, que podem ser pensadas como duas notações que representam a mesma estrutura. Na chamada configuração anversa usual, os pontos de rede adicionais estão nas coordenadas (2⁄3, 1⁄3, 1⁄3) e (1⁄3, 2⁄3, 2⁄3), enquanto na configuração reversa alternativa eles estão nas coordenadas (1⁄3,2⁄3,1⁄3) e (2⁄3,1⁄3,2⁄3). Em ambos os casos, existem 3 pontos de rede por célula unitária no total e a rede não é primitiva.[3]
As redes de Bravais na família dos cristais hexagonais também podem ser descritas por eixos romboédricos. A célula unitária é um romboedro (que dá o nome para a rede romboédrica). Esta é uma célula unitária com parâmetros a = b = c; α = β = γ ≠ 90°. Na prática, a descrição hexagonal é mais comumente usada porque é mais fácil lidar com um sistema de coordenadas com dois ângulos de 90°. No entanto, os eixos romboédricos são freqüentemente mostrados (para a rede romboédrica) em livros didáticos porque esta célula revela a simetria de 3m da rede cristalina.[4][5]
A célula unitária romboédrica para a rede hexagonal de Bravais é a célula centrada em D consistindo de dois pontos de rede adicionais que ocupam uma diagonal de corpo da célula unitária com coordenadas (1⁄3, 1⁄3, 1⁄3) e (2⁄3, 2⁄3, 2⁄3). No entanto, essa descrição raramente é usada.[4][5]
Referências
- ↑ BRANCO, Pércio de Moraes. Dicionário de Mineralogia e Gemologia. São Paulo: Oficina de Textos, 2008. 608 p. il.
- ↑ https://books.google.com/books?id=e7MSMwEACAAJ
- ↑ a b Edward Prince (2004). Mathematical Techniques in Crystallography and Materials Science. [S.l.]: Springer Science & Business Media. p. 41
- ↑ a b «Medium-Resolution Space Group Diagrams and Tables». img.chem.ucl.ac.uk
- ↑ a b Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics 1st ed. [S.l.]: Holt, Rinehart and Winston. p. 119. ISBN 0-03-083993-9