Modelo FitzHugh–Nagumo
O modelo FitzHugh–Nagumo é um dos principais modelos de disparos neuronais, ou seja, um dos principais modelos matemáticos que descrevem o formato do potencial de ação gerado nos neurônios. O modelo em questão faz referência a Richard FitzHugh (1922 – 2007), que sugeriu a criação do sistema em 1961[1] e a J. Nagumo et al., que criou o circuito equivalente no ano seguinte,[2] descrevendo o protótipo de um sistema excitável, por exemplo, o de um neurônio.
O modelo pode ser visto como uma versão simplificada do modelo de Hodgkin-Huxley,[3] que por sua vez, faz uma modelagem mais detalhada da ativação e desativação dos canais iônicos envolvidos na geração de um disparo neuronal. Nos artigos originais de FitzHugh, esse modelo foi chamado de oscilador Bonhoeffer–van der Pol (em homenagem a Karl Friedrich Bonhoeffer e Balthasar van der Pol), por ser uma generalização do anteriormente descrito oscilador de Van der Pol,[4] sendo este um caso específico com os parâmetros .
Modelo
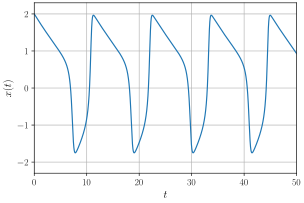
editarO modelo de FitzHugh–Nagumo é um exemplo de sistema dinâmico excitatório-oscilatório com duas variáveis de estado. A principal delas, , é a variável relacionada ao potencial de membrana, enquanto é responsável pela acomodação e resistência do sistema. Quanto aos parâmetros envolvidos, e são constantes que determinam o percurso descrito pelo sistema no espaço de fase, é uma constante adicionada por conveniência ainda no oscilador de Van der Pol e pode ser compreendido como um estímulo externo injetado no neurônio. Sendo assim, com exceção de , os parâmetros não possuem equivalência com algum fenômeno biológico e são escolhidos apenas para se obter o formato semelhante ao de um disparo neuronal em .
O sistema de equações diferenciais ordinárias que rege esse modelo dinâmico é
- ,
em que e representam, respectivamente, as primeiras derivadas temporais das variáveis e .
Descrição
editarPara que o modelo apresente o comportamento esperado, os parâmetros devem obedecer às condições , e .
Nesse caso, a dinâmica do sistema pode ser descrita pelo zapping, uma alternância rápida, entre os ramos esquerdo e direito da nullcline cúbica referente à variável . Além dessa, o sistema também apresenta uma nullcline linear referente à variável . Ambas equações podem ser obtidas ao se igualar e a zero, resultando no par de equações
- ,
cuja intersecção dessas curvas é o ponto de equilíbrio do sistema.
Ver também
editarLeituras adicionais
editar- FitzHugh R. (1955) Mathematical models of threshold phenomena in the nerve membrane. Bull. Math. Biophysics, 17:257—278
- FitzHugh R. (1969) Mathematical models of excitation and propagation in nerve. Chapter 1 (pp. 1–85 in H.P. Schwan, ed. Biological Engineering, McGraw–Hill Book Co., N.Y.)
Ligações externas
editar- O Modelo FitzHugh–Nagumo na Scholarpedia
- Interactive FitzHugh-Nagumo. Aplet Java, inlcuindo espaço fásico e parâmetros que podem ser editados em qualquer tempo.
- Interactive FitzHugh–Nagumo in 1D. Aplet Java para simular ondas 1D propagando numa estrutura anelar. Os parâmetros podem ser alterados.
- Interactive FitzHugh–Nagumo in 2D. Aplet Java para simular ondas 2D, inlcuindo ondas em espiral. Os parâmetros podem ser alterados.
- Java applet for two coupled FHN systems Options include time delayed coupling, self-feedback, noise induced excursions, data export to file. Source code available (BY-NC-SA license).
Referências
- ↑ FitzHugh, Richard (julho de 1961). «Impulses and Physiological States in Theoretical Models of Nerve Membrane». Biophysical Journal (6): 445–466. ISSN 0006-3495. doi:10.1016/s0006-3495(61)86902-6. Consultado em 28 de abril de 2023
- ↑ Nagumo, J.; Arimoto, S.; Yoshizawa, S. (outubro de 1962). «An Active Pulse Transmission Line Simulating Nerve Axon». Proceedings of the IRE (10): 2061–2070. ISSN 0096-8390. doi:10.1109/jrproc.1962.288235. Consultado em 28 de abril de 2023
- ↑ Hodgkin, A. L.; Huxley, A. F. (1952). «A quantitative description of membrane current and its application to conduction and excitation in nerve». The Journal of physiology (em inglês). 117 (4): 500-544. ISSN 0022-3751. doi:10.1113/jphysiol.1952.sp004764. Consultado em 27 de abril de 2023
- ↑ van der Pol, B (1926). «On "Relaxation-Oscillations"». Taylor & Francis. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 2 (11): 978-992. doi:10.1080/14786442608564127. Consultado em 27 de abril de 2023







