Modelo Hindmarsh-Rose
O modelo Hindmarsh–Rose é um modelo de atividade neuronal proposto por J. L. Hindmarsh e R. M. Rose em 1984[1] que tem como objetivo estudar o comportamento de rajada de disparos do potencial de membrana observado em experimentos feitos com um único neurônio.
A principal variável do modelo, , refere-se ao potencial de membrana, que assim como as demais variáveis, é descrito em unidades adimensionais. Além desta, o modelo apresenta mais duas variáveis, e , que levam em conta o transporte de íons através da membrana por meio de canais iônicos. O transporte de íons de sódio e potássio é feito por canais rápidos e a sua taxa é medida por , nomeada por variável de spiking. O transporte de outros íons, como o cálcio, é feito através de canais lentos, e é representado por , que recebe o nome de variável de rajada. O modelo apresenta oito parâmetros: , , , , , , e . Contudo, apenas possui uma relação com algum fenômeno biológico, uma vez que pode ser compreendido como uma corrente injetada sobre o neurônio como estímulo externo.
O modelo de Hindmarsh–Rose é o sistema com três equações diferenciais ordinárias não-lineares
- ,
em que , e representam, respectivamente, as primeiras derivadas temporais das variáveis , e .
Análise
editarAs duas primeiras equações do modelo estão envolvidas com o comportamento de disparo. Sendo assim, os parâmetros , , , modelam o trabalho dos canais rápidos de íons. Geralmente esses parâmetros são fixados ao simular o modelo, caso sejam adotados os valores do artigo original[1], os valores são , , e . Dessa forma, pode-se adotar como parâmetro de controle, o que significa que a corrente que entra no neurônio pode variar.
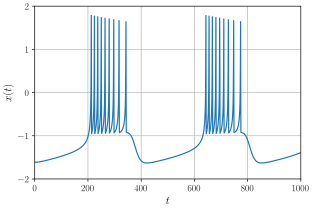
A terceira equação de estado permite uma grande variedade de comportamentos dinâmicos do potencial de membrana, descritos pela variável . Sua ação no modelo pode ser comparada ao processo de hiperpolarização pelo qual o potencial de membrana passa após gerar um disparo. O parâmetro , dado que este é responsável pela demora dos canais lentos, normalmente assume valores pequenos da ordem de . Com frequência, os parâmetros mantidos fixos são e . Dessa forma, o modelo de Hindmarsh–Rose fornece uma boa descrição qualitativa dos muitos padrões diferentes que são observados empiricamente, incluindo um comportamento imprevisível conhecido como dinâmica caótica, de maneira relativamente simples.
Ver também
editarReferências
- ↑ a b Hindmarsh, J. L.; Rose, R. M. (22 de março de 1984). «A model of neuronal bursting using three coupled first order differential equations». Proceedings of the Royal Society of London. Series B. Biological Sciences (1222): 87–102. ISSN 0080-4649. doi:10.1098/rspb.1984.0024. Consultado em 3 de maio de 2023






















![{\displaystyle {\begin{cases}{\dot {x}}(t)=-ax^{3}(t)+bx^{2}(t)+y(t)-z(t)+I\\{\dot {y}}(t)=c-dx^{2}(t)-y(t)\\{\dot {z}}(t)=r[s(x(t)-x_{R})-z(t)]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bbe289ab7874582f3bdc5fb9f734c3552184c9c)


