Pomar de Euclides

Em matemática, informalmente falando, o pomar de Euclides é uma matriz de uma matriz de "árvores" unidimensionais de altura um plantadas nos pontos de um quadrante de um reticulado quadrado. Mais formalmente, o pomar de Euclides é o conjunto de segmentos de reta ligando (i, j, 0) a (i, j, 1), em que i e j são inteiros positivos.

Um canto do pomar de Euclides, em que as árvores estão marcadas com a coordenada x de sua projeção sobre o plano x + y = 1.

Vista plana de um canto do pomar de Euclides. As árvores marcadas por um ponto azul sólido são visíveis a partir da origem.

Vista em perspectiva do pomar de Euclides a partir da origem. As árvores em vermelho indicam as linhas a duas unidades da diagonal principal.

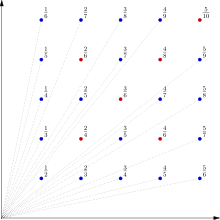
As árvores visíveis a partir da origem são aquelas nos pontos (m, n, 0) do reticulado, em que m e n são primos entre si, isto é, tais que a fração mné irredutível. O nome pomar de Euclides é derivado do algoritmo de Euclides.

Se o pomar é projetado em relação à origem sobre o plano x + y = 1 (ou, equivalentemente, desenhado em perspectiva por um observador situado na origem) as copas das árvores formam um gráfico da função de Thomae. O ponto (m, n, 1) é projetado em

$\left({\frac {m}{m+n}},{\frac {n}{m+n}},{\frac {1}{m+n}}\right).$

Ver também

• Problema da floresta opaca

Ligações externas

• Folha de atividades e problemas para 9-11 sobre o pomar de Euclides, da Texas Instruments, Inc.
• Problema relacionado no projeto Euler