Quebra de simetria
Na física, quebra de simetria é um fenômeno em que um estado desordenado e simétrico colapsa em um estado ordenado, porém menos simétrico.[1] Esse colapso é frequentemente uma das muitas bifurcações possíveis que uma partícula pode assumir ao se aproximar de um menor estado de energia. Devido às diversas possibilidades, um observador pode assumir que o resultado do colapso é arbitrário. Esse fenômeno é fundamental para a teoria quântica de campos (TQC) e para os entendimentos contemporâneos de física.[2] Especificamente, desempenha um papel central no modelo Glashow-Weinberg-Salam, que faz parte do modelo padrão, modelando o setor eletrofraco.


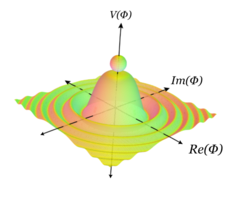
Em um sistema infinito (espaço-tempo de Minkowski), ocorre quebra de simetria. Entretanto em um sistema finito (isto é, qualquer sistema real supercondensado), o sistema é bem menos previsível, mas em muitos casos ocorre tunelamento quântico.[2][3] Quebra de simetria e tunelamento se relacionam através do colapso de uma partícula em estados não-simétricos, enquanto a partícula procura um menor estado de energia.[4]
A quebra de simetria pode ser distinguida em dois tipos: explícita e espontânea. Elas são assim caracterizados ou pelas suas equações de movimento falharem em ser invariantes, ou pelo seu estado fundamental falhar em ser invariante.
Descrição não-técnica
editarNesta seção é descrita a quebra de simetria espontânea. Em termos leigos, esta é a ideia de que, para um sistema físico, a configuração de energia mais baixa (o estado de vácuo) não é a configuração mais simétrica do sistema. Basicamente, existem três tipos de simetria que podem ser quebradas: discreta, contínua e de calibre (ordenadas em crescente tecnicidade).
Um exemplo de sistema com simetria discreta pode ser dada pela figura com a curva do gráfico vermelha: considere uma partícula movendo-se nesta curva, sujeita à ação da gravidade. Um gráfico semelhante poderia ser obtido pela função . Este sistema é simétrico sob reflexão no eixo y. Existem, portanto, três possíveis estados estacionários para a partícula: o topo da colina em , ou na parte inferior, em . Quando a partícula está no topo a configuração respeita a simetria da reflexão: a partícula fica no mesmo lugar quando refletida. Porém, as configurações de menor energia são aquelas em (onde a partícula apresenta menor energia potencial gravitacional). Quando a partícula está em qualquer uma dessas configurações, ela não está mais fixa sob reflexão no eixo y, ou seja, a reflexão troca os dois estados de vácuo.
Um exemplo com simetria contínua é dado por um análogo 3d do exemplo anterior, ao se rotacionar o gráfico em torno de um eixo através do topo da colina. A superfície obtida é dada igualmente pelo gráfico de . Esse é, essencialmente, o gráfico do potencial do chapéu mexicano. O gráfico possui uma simetria contínua dada pela rotação em torno do eixo através do topo da colina (bem como uma simetria discreta por reflexão através de qualquer plano radial). Novamente, se a partícula está no topo da colina ela é fixada em rotações, tendo porém, maior energia gravitacional. No fundo, não é mais invariante sob rotações, mas minimiza sua energia potencial gravitacional. Além disso, as rotações movem a partícula de uma configuração de minimização de energia para outra. Há uma novidade aqui, não vista no exemplo anterior: a partir de qualquer um dos estados de vácuo é possível acessar qualquer outro estado de vácuo com apenas uma pequena quantidade de energia, movendo-se ao redor da calha na base da colina. Já no exemplo anterior, para acessar o outro vácuo a partícula teria que atravessar o topo do gráfico, o que exige uma enorme quantidade de energia.
A quebra da simetria de Gauge é a mais sutil, porém tem importantes consequências físicas. Grosso modo, para os propósitos desta seção, uma simetria de Gauge é uma atribuição de sistemas com simetria contínua a todos os pontos do espaço-tempo. A simetria de Gauge proíbe a geração de massa para campos de Gauge. Mesmo assim, campos de Gauge maciços (bósons W e Z) foram observados. A quebra espontânea de simetria foi desenvolvida para resolver tal inconsistência. A ideia é que, em um estágio inicial, o universo estava um estado de alta energia (análogo à partícula no topo da colina) e, consequentemente, tinha simetria de Gauge total e todos os campos de Gauge não possuiam massa. À medida que esfriava, ele se acomodava em uma escolha de vácuo, quebrando assim espontaneamente a simetria, removendo dessa forma a simetria de Gauge e permitindo a geração de massa desses campos de Gauge. Uma explicação completa é altamente técnica (veja interação eletrofraca).
Quebra espontânea de simetria
editarNa quebra espontânea de simetria (QES), as equações de movimento do sistema são invariantes. Porém, qualquer estado de vácuo (estado de menor energia) não é invariante.
Um exemplo com simetria dupla seria um átomo que tenha dois estados de vácuo. Ao se ocupar qualquer um desses dois estados, há uma quebra dessa simetria dupla. Esse ato de selecionar um dos estados conforme o sistema atinge uma energia mais baixa é a quebra espontânea de simetria. Quando isso ocorre, o átomo não é mais simétrico (reflexivamente simétrico), tendo colapsado para um estado de energia inferior.
Tal quebra de simetria é parametrizada pelo parâmetro de ordem. Um caso especial desse tipo de quebra de simetria é a chamada quebra de simetria dinâmica.
No cenário Lagrangiano da teoria quântica de campos (TQC), o Lagrangiano é um funcional de campos quânticos que é invariante sob a ação de um grupo de simetria . No entanto, o valor esperado do vácuo formado quando a partícula colapsa para uma energia mais baixa pode não ser invariável sob . Neste caso, haverá uma quebra parcial da simetria de em um subgrupo . Isso é o que se chama de quebra de simetria espontânea.
Porém, no contexto de simetria de Gauge, quebra espontânea de simetria é o fenômeno pelo qual os campos de Gauge "adquirem massa", apesar da invariância de Gauge impor que tais campos não têm massa. Isso ocorre porque a QES da simetria de Gauge quebra a invariância de Gauge. Tal quebra permite a existência de campos de Gauge maciços. Esta é uma exceção importante do Teorema de Goldstone, onde um bóson Nambu-Goldstone pode ganhar massa, tornando-se um bóson de Higgs no processo.[5]
Além disso, neste contexto o uso do termo "quebra de simetria" é incorreto , já que "simetria" de gauge não é realmente uma simetria, mas uma redundância na descrição do sistema. Matematicamente, essa redundância é uma escolha de trivialização, algo análogo à redundância decorrente de uma escolha de base.
A quebra espontânea de simetria também está associada às transições de fase. Por exemplo, no modelo de Ising, à medida que a temperatura do sistema cai abaixo da temperatura crítica, a simetria de vácuo é quebrada, dando ao sistema uma transição de fase.
Quebra de simetria explícita
editarNa quebra de simetria explícita (QSE), as equações de movimento que descrevem um sistema são variantes sob a simetria quebrada. No caso da mecânica Hamiltoniana (ou mecânica Lagrangiana) isso acontece quando há pelo menos um termo no hamiltoniano (ou Lagrangiano) que explicitamente quebra a simetria dada.
No cenário hamiltoniano, esse fenômeno é frequentemente estudado quando o Hamiltoniano pode ser escrito como .
Nessa equação, o termo é um "Hamiltoniano de base", que tem alguma simetria manifesta. Mais explicitamente, é simétrico sob a ação de um grupo de Lie . Muitas vezes, este é um hamiltoniano integrável.
O termo é uma perturbação ou interação Hamiltoniana. Ele não é invariável sob a ação de . Geralmente é proporcional a um (pequeno) parâmetro perturbativo.
Este é essencialmente o paradigma para a teoria da perturbação na mecânica quântica. Um exemplo de seu uso é encontrar a estrutura fina dos espectros atômicos.
Exemplos
editarA quebra de simetria pode abranger qualquer um destes cenários:
- A quebra de uma simetria exata das leis subjacentes da física pela formação aparentemente aleatória de alguma estrutura;
- Uma situação na física em que um estado mínimo de energia possui menos simetria do que o próprio sistema;
- Situações em que o estado real do sistema não reflete as simetrias subjacentes da dinâmica porque o estado manifestamente simétrico é instável (a estabilidade é obtida à custa da assimetria local);
- Situações em que as equações de uma teoria podem ter certas simetrias, embora suas soluções não possam (as simetrias estão "ocultas").
Um dos primeiros casos de quebra de simetria discutido na literatura física está relacionado à forma assumida por umfluido incompressível em rotação uniforme, equilíbrio gravitacional e equilíbrio hidrostático. Jacobi[6] e logo depois Liouville,[7] discutiram, em 1834, o fato de que um elipsóide tri-axial era uma solução de equilíbrio para esse problema quando a energia cinética comparada à energia gravitacional do corpo em rotação excedia um certo valor crítico. A simetria axial apresentada pelos esferóides de McLaurin é quebrada neste ponto de bifurcação. Além disso, acima deste ponto de bifurcação (e para momento angular constante) as soluções que minimizam a energia cinética são os elipsóides de Jacobi não-axialmente simétricos, ao invés dos esferóides de Maclaurin.
Veja também
editarReferências
editar- ↑ Heylighen, Francis (20 de março de 2021). «Entanglement, Symmetry Breaking and Collapse: Correspondences Between Quantum and Self-Organizing Dynamics». Brussels, Belgium. Foundations of Science: 85-107 – via SpringerLink
- ↑ a b Gross, David J. (10 de dezembro de 1996). «The role of symmetry in fundamental physics». PNAS. 93 (25). Consultado em 28 de fevereiro de 2023
- ↑ Ohira, Ryutaro; Mukaiyama, Takashi; Toyoda, Kenji (1 de fevereiro de 2020). «Breaking rotational symmetry in a trapped-ion quantum tunneling rotor» 2 ed. Physical Review A. American Physical Society. 101 (2). arXiv:1907.07404 – via SAO/NASA Astrophysics Data System
- ↑ Castellani, Elena; Teh, Nicholas; Brading, Katherine (14 de dezembro de 2017). Edward, Zalta, ed. «Symmetry and symmetry breaking» Fall 2021 ed. Metaphysics Research Lab, Stanford University. Stanford Encyclopedia of Philosophy
- ↑ Law, Johnathan; Rennie, Richard (2009). «Goldstone's theorem». A Dictionary of Physics 6 ed. [S.l.]: Oxford University Press. ISBN 9780199233991. doi:10.1093/acref/9780199233991.001.0001. Consultado em 1 de março de 2023
- ↑ Jacobi, C.G.J. (1834). «Über die figur des gleichgewichts». Annalen der Physik und Chemie. 109 (33): 229–238. Bibcode:1834AnP...109..229J. doi:10.1002/andp.18341090808
- ↑ Liouville, J. (1834). «Sur la figure d'une masse fluide homogène, en équilibre et douée d'un mouvement de rotation». Journal de l'École Polytechnique (14): 289–296
Ligações externas
editar- O Wikiquote possui citações de ou sobre: Symmetry breaking
